(Non-exhaustive) List of Training-Free Samplers
At the beginning of each section, you may find a table summarizing the samplers mentioned in the section.
| Sampler | Time Spent | Order | Converges | Notes |
|---|---|---|---|---|
| Name of the sampler | How many times slower than euler. 1x=the same as euler, 2x=takes twice as long as euler, etc |
The order, as mentioned in #accuracy/control. Some technically support a range of orders, in that case, I'll include the default & range. | Yes (refines 1 image with more steps) / No (may change composition with more steps) | Some notes about the sampler |
Explicit Runge-Kutta Methods: Euler, Heun, and Beyond
| Sampler | Time Spent | Order | Converges | Notes |
|---|---|---|---|---|
euler |
1x | 1 | Yes | Simplest and most inaccurate, makes soft lines & blurs details. |
euler_ancestral |
1x | 1 | No | Like euler but divergent (adds noise), popular. |
heun |
2x | 2 | Yes | Can be thought of as the "improved" euler |
bosh3 |
3x | 3 | Yes | 3rd order RK |
rk4 |
4x | 4 | Yes | 4th order RK |
dopri6 |
6x | 5 | Yes | 6 model calls/step is needed for order 5. |
euler, heun, and the rarer fehlberg2, bosh3, rk4, dorpi6, and more, all fall under the umbrella of explicit Runge-Kutta(RK) Methods for solving ODEs. They were developed way before any diffusion model, or even any modern computer, came to be.
RK methods are singlestep, which means that the higher order ones take a while to run. bosh3 for example takes 3 times longer than euler per step. Combined with the fact that diffusion DEs are stiff, this means that it's seldom worth using a high-order explicit RK method by itself, as it massively increases sampling time while netting you a very marginal gain in quality.
Personally, I'd at most use bosh3, though even that's cutting it close. It's no wonder that you don't find some of these in popular UIs.
Samplers developed down the road employ optimizations specific to diffusion equations, making them the better choice 90% of the time.
Where Can I Find Higher Order RK Samplers?
- ComfyUI: ComfyUI-RK-Sampler or RES4LYF
- reForge: Settings->Sampler according to this
Early Days of Diffusion: DDPM, DDIM, PLMS(PNDM)
| Sampler | Time Spent | Order | Converges | Notes |
|---|---|---|---|---|
ddpm |
1x | 1 | No | The original diffusion sampler |
ddim |
1x | 1 | Yes | Converges faster than DDPM, trading a bit of quality |
plms=pndm |
1x | default 4 (up to 4) | Yes | LMS tailored for use in diffusion (uses Adams–Bashforth under the hood) |
DDPM was what started it all, applying diffusion models to image generation, achieving really high quality but requiring a thousand steps to generate a sample.
Through adjustments to the diffusion equation, people arrived at DDIM, drastically reducing the number of steps required at the cost of a little quality.
PNDM finds that classical methods don't work well with diffusion equations. So they design a new way to do it - pseudo numerical methods. They then tried many approaches and found that Pseudo Linear Multistep Method (PLMS) seemed the best, hence the other name.
These 3, along with the classical ODE solvers euler, heun, and LMS, were the original samplers shipped with the release of the original stable diffusion.
Steady Improvements: DEIS + iPNDM, DPM
| Sampler | Time Spent | Order | Converges | Notes |
|---|---|---|---|---|
deis |
1x | default 3 (up to 4) | Yes | |
ipndm |
1x | 4 | Yes | ipndm found empirically better than ipndm_v |
ipndm_v |
1x | 4 | Yes | |
dpm_2 |
2x | 2 | Yes | |
dpm_2_ancestral |
2x | 2 | No | |
dpm_adaptive |
3x | default 3 (2 or 3) | Yes | ignores steps & scheduler settings, runs until it stops itself |
dpm_fast |
1x (averaged) | between 1~3 | Yes | Uses DPM-Solver 3,2,1 such that the number of model calls = number of steps, effectively taking the same time as euler would in the same number of steps |
DEIS and DPM independently came to the same conclusion: Diffusion equations are too stiff for classical high-order solvers to do well. They use a variety of techniques to remedy this. Notably, they both solve a part of the equation exactly, removing any error associated with it while leaving the rest less stiff. This idea is so good in fact that many samplers down the road also do it.
The DEIS paper also introduced "improved PNDM" (iPNDM). ipndm_v is the variable step version that should work better for diffusion, though they find empirically that ipndm performs better than ipndm_v.
Differing Results With ipndm_v
In my personal tests in ComfyUI, for some reason, I find for the same exact parameters - prompt, seed, etc. - ipndm_v sometimes breaks (lots of artifacts) if you use KSampler, but not if you use SamplerCustomAdvanced. In fact, I've never gotten any image breakdown with SamplerCustomAdvanced + ipndm_v, unless at low steps where it hasn't converged.
Bextoper has also noted that ipndm_v breaks similarly to KSampler in Forge.
Cascade of New Ideas: DPM++, UniPC, Restart, RES, Gradient Estimation, ER SDE, SEEDS
| Sampler | Time Spent | Order | Converges | Notes |
|---|---|---|---|---|
dpmpp_2s_ancestral |
2x | 2 | No | "dpmpp" as in "DPM Plus Plus" = "DPM++" |
dpmpp_sde |
2x | 2 | No | I think this is "SDE-DPM-Solver++(2S)" not found explicitly defined in the paper |
dpmpp_2m |
1x | 2 | Yes | |
dpmpp_3m_sde |
1x | 3 | No | |
uni_pc |
1x | 3 | Yes | Official repo |
uni_pc_bh2 |
1x | 3 | Yes | Empirically found a little better than uni_pc in guided sampling |
Restart |
default 2x (varies) | default 2 (varies) | No | Time Spent & order depends on the underlying solver used (paper uses heun); Official repo |
res_multistep |
1x | 2 | Yes | The authors give a general way to define res_singlestep for any order |
gradient_estimation |
1x | 2 (?) | Yes | Uses 2 substeps, so I guess order 2? Not sure if the notion of order really applies... |
seeds_2/3 |
2/3x | 2/3 | No | |
er_sde |
1x | default 3 (1-3) | No | Official repo |
*(this nothing to do with StableCascade I just thought it's a cool title)
Around this time, the idea of guidance took off, offering the ability to specify what image we want to generate, but also bringing new challenges to the table:
- High guidance makes the DE even stiffer, breaking high-order samplers
- High guidance knocks samples out of the training data range (train-test mismatch), creating unnatural images
To address issues with high CFG, DPM++ adds 2 techniques (that were proposed in prior works by others already) to DPM:
- Switch from noise (eps, \(\epsilon\)) prediction to data (\(x_0\)) prediction (which they show is better by a constant in Appendix B).
- The above also allows them to apply thresholding to push the sample back into training data range.
Practical; Not a Technical Marvel
The dpmpp family, especially dpmpp_2m, are one of the most widely used samplers alongside euler_ancestral. However, it was rejected by ICLR due to heavily relying on existing works, so it "does not contain enough technical novelty."
UniPC came soon after. Inspired by the predictor-corrector ODE methods, they develop UniC, a corrector that can be directly plugged after any existing sampler to increase its accuracy. As a byproduct, they derive UniP from the same equation as UniC, which is a predictor that can go up to any arbitrary order. The two combine to UniPC, achieving SOTA results using order=3.
Restart doesn't actually introduce a new sampler, instead focusing on the discrepancy between trying to solve diffusion as an ODE (no noise injections) vs. an SDE (injects noise at every step). To get the best of both worlds, Restart proposes that rather than injecting noise at every step, let's do it in infrequent intervals.
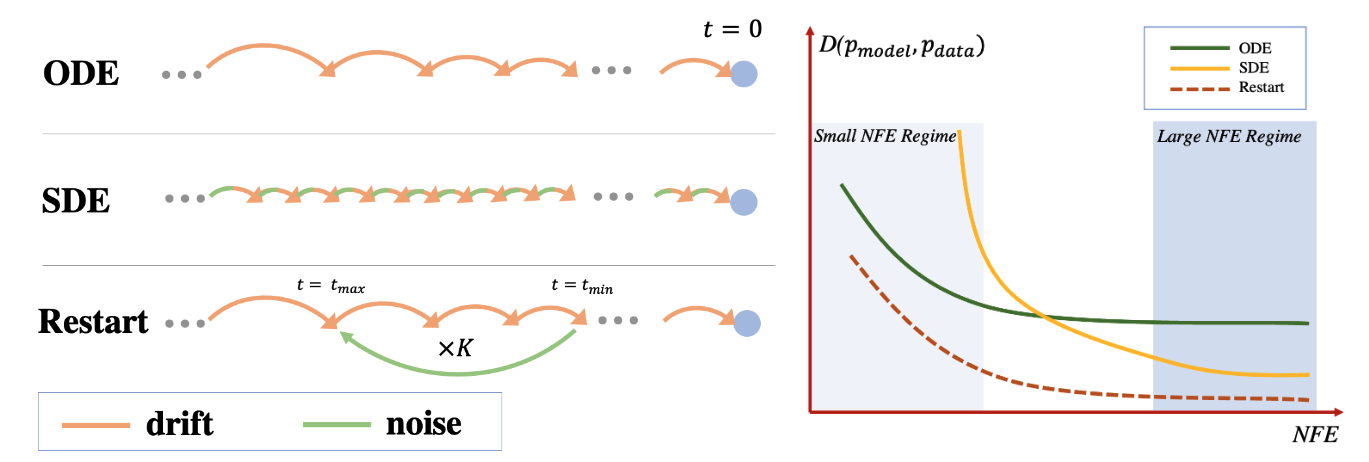
RES identified an overlooked set of conditions that solvers must satisfy to achieve their claimed order (they find that dpmpp doesn't satisfy some of these, leading to worse-than-expected results). They then unify the equation for noise prediction and data prediction, making analysis easier. Finally, they pick coefficients that satisfy these additional conditions.
Gradient Estimation finds that denoising can be interpreted as a form of gradient descent, and designs a sampler based on it.
SEEDS rewrites a whole lot of equations so that more parts can be solved exactly or approximated more accurately. To make sure the equation stays true, a modified way of injecting noise is used. They derive SEEDS for both eps-pred and data-pred, though the former is very slow so ComfyUI includes only the latter.
ER SDE models the diffusion process as an Extended Reverse-Time SDE and develops a solver based on that.
Out of Reach: AMED, DC-Solver, among Others
With so many samplers, it's no surprise that some have been left out of the party. This section includes sampling techniques that, while exist in literature or python code, are unavailable in popular UIs that are more accessible to non-coders. Since they're not widely available, discussion is also low so there will be many more that I simply don't know about and are missing from the list.
Techniques Not Included: (in no particular order)
- UniC: As said before, you could in theory plug UniC after any sampler to achieve better accuracy. No UI lets you actually do that though to my knowledge.
Samplers Not Included: (in no particular order)